Graph (Network - Nodes and edges)
About
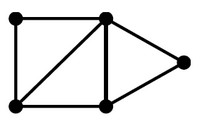
A graph is a set of vertices connected by edges. See Graph - Graph Model (Network Model)
Data representation that naturally captures complex relationships is a graph (or network).
Except of the special graph that a tree is, the data structure of a graph is non-hierarchical.
Points are called nodes, links are called edges. A link can only connect two nodes (only binary relationship ?)
Each edge has two endpoints, the nodes it connects. The endpoints of an edge are neighbors.
See also: (Graph|Network) - Database
Application
Are mostly graphs:
Type
- Graph - Acyclic - graphs that do/don't allow self-loops.
- graphs whose nodes/edges are insertion-ordered, sorted, or unordered
Structure
Graph data structure explained: Graph - Data Structure (Physical Representation)
Example
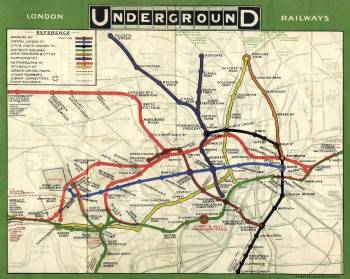
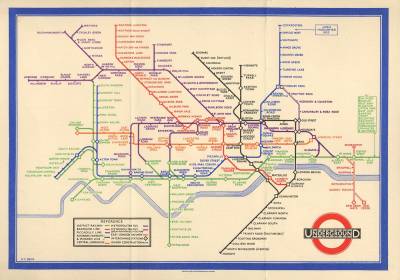
Map
Directed Graph
(Network|Graph) - Directed acyclic graph (DAG)
Dominating set
A dominating set in a graph is a set S of nodes such that every node is in S or a neighbor of a node in S.
Neither algorithm is guaranteed to find the smallest solution.
Grow Algorithm
initialize S = 0;
while S is not a dominating set,
add a node to S.
Shrink Algorithm
initialize S = all nodes
while there is a node x such that S −{x} is a dominating set,
remove x from S
Path
Definition
Cycle
A x-to-x path is called a cycle
Spanning
A set S of edges is spanning for a graph G if, for every edge {x, y} of G, there is an x-to-y path consisting of edges of S.
Forest
A set of edges of G is a forest if the set includes no cycles.
Analysis
See Graph - Analysis