About
Mediation is a different multivariate than moderation approach called mediation. mediation and moderation are very different kinds of analysis used to address very different types of questions.
A mediator explains the relationship between a predictor and outcome (or an independent variable and a dependent variable). Generally X and Y.
The mediator is the mechanism through which the effect occurs.
The main reason to run a mediation analysis is to better understand the correlation between two variables.
The point of this analysis is to say, what accounts for the relationship between the variables.
Articles Related
Formal definition
A mediation analysis is typically conducted to better understand:
- in experimental research: the observed effect of an independent variable on a dependent variable
- in correlational research: a correlation between X and Y.
One of the problems or limitations with correlational research is correlation does not imply causation. So it's very difficult to get at mechanisms underlying correlations. Mediation is one tool to do that.
Approach
Standard
The standard approach is via a series of multiple regressions.
If we have a correlation between X and Y we can introduce a mediator variable to see if it can account for that relationship. Which might lead to stronger claims about causality. If two variables are correlated because of the mediator, X should predict M and in turn M should predict Y.
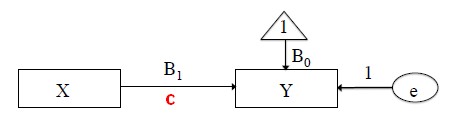
<math> \begin{array}{rrl} Y & = & B_0 + B_1X + e & \text{X and Y have to be correlated, the regression coefficient for X should be significant}\\ M & = & B_0 + B_1X + e & \text{M and X have to be correlated, the regression coefficient for X should be significant}\\ Y & = & B_0 + B_1X + B_2M + e & \text{The regression coefficient for X should be significant and what happens for X ?} \end{array} </math>
The direct effect is the effect on Y from X
The important thing to watch is what happens to the regression coefficient for X on this equations. If the regression coefficient for X:
- suddenly drops, that means it's explained by the mediator (There is no mediation).
- remains the same (ie significant and strong in the third equation), the mediator isn't doing probably anything. (There is probably mediation)
Type
Expected no mediation, a mediator variable accounts for some or all of the relationship:
Full
Full mediation accounts for ALL the variance between X and Y. In that situation you would see the regression coefficient for X drop all the way to zero.
The direct effect is no longer significant after adding the mediator in the regression equation.
The sobel test is significant.
Partial
Partial Mediation accounts for some of the variance. You'll see a drop in the regression coefficient associated with X. But you won't see it drop all the way to zero and it, it might remain significant.
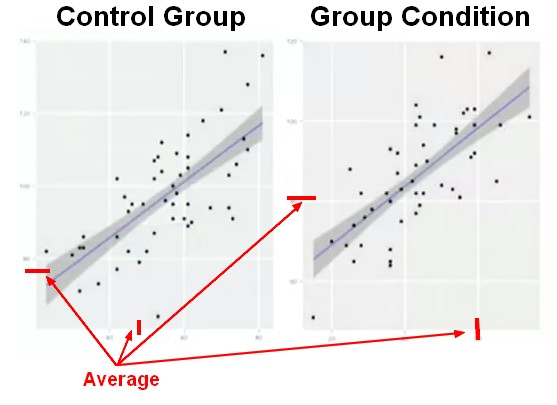
Visualisation
The group condition is doing worse on both variable and the relationship between the two variables holds, that doesn't change. The regression line is the same. It's a difference from moderation analysis.
The point of this analysis is to say, what accounts for the relationship between the variables.
Path analysis
Path analysis is a sort of different approach, to the data. It falls under different mathematical framework called Structural Equation Modeling, rather than the General Linear Model.
Path models are often used to illustrate mediation whereas Structural Equation Modeling is used to analyze mediation.
Mediation analyses are typically illustrated using “path model”.It is a graphical model that depicts the results of the regressions of the standard approach.
Path models are:
- a form of structural equation models (Advanced Topic in Statistics)
- graphical models with a grammar where:
- rectangles represent observed variables (X, Y, M)
- Circles represent unobserved variables. The things we just can't observe or don't see. (In this case, the error term (e))
- Triangles are used to represent constants.
- Arrows represent associations between variables
Simple Regression
In a true structural equation modeling, a directional arrow implies causality.
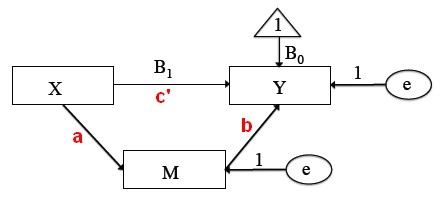
Simple Regression with Mediator
Standard Path Label:
- a: Path from X to M
- b: Path from M to Y
- c: Direct Path from X to Y (before including M)
- c': Direct Path from X to Y (after including M)
- Note: (a*b) is known as the indirect path
Sobel
It's a lot easier to explain what the Sobel test is doing with labels on these paths.
The Sobel test is testing the effect of the indirect path (from X through M to Y) to see if it's statistically significant. Its a null hypothesis significance test were the null hypothesis is that the indirect effect is 0.
As any other sort of NHST, the equation is a ratio basically, of what we observed relative to what we would expect due to chance. If we get two or three times more than what we would expect due to chance, we're going to reject the null.
<MATH> z=\frac{(B_a*B_b)}{\sqrt{({B_a}^2+{\href{standard_error}{SE}_b}^2)+({B_b}^2+{\href{standard_error}{SE}_a}^2)}} </MATH>
The Sobel test is not testing the change from c to c-prime. It's testing the null hypothesis that the indirect effect is 0 <math>B_a*B_b=0</math> . If we get a nice strong indirect effect, indicating mediation, then the null hypothesis will be rejected. The null hypothesis of the Sobel test is the indirect effect of X on Y with a mediator variable M is zero.
The Sobel tests gives:
- a regression coefficient <math>B_a*B_b=0</math>
- the z score. To be significant with an alpha of .05 in a z-test. we need a score beyond 1.96.
- the sample size.