About
Vector Vector Operations:
- translation (also known as addition or substraction)
- scalar_multiplication (Scaling)
Articles Related
List
Using operator overloading, you can compute this operations with the following syntax.
| Operation | Syntax |
|---|---|
| vector addition | u+v |
| vector negation | -v |
| vector subtraction | u-v |
| scalar-vector multiplication | alpha*v |
| division of a vector by a scalar | v/alpha |
| dot-product | u*v |
| getting value of an entry | v[d] |
| setting value of an entry | v[d] = … |
| testing vector equality | u == v |
| pretty-printing a vector | print(v) |
| copying a vector | v.copy() |
Operations
Translation
A vector translation is also known as a vector Addition.
Syntax
[u1, u2, . . . , un] + [v1, v2, . . . , vn] = [u1 + v1, u2 + v2, . . . , un + vn]
v + 0 = v
Property
Vector addition is
(x + y) + z = x + (y + z)
- and (Function|Operator) - Algebraic (Laws|properties) - Axioms. The order doesn't matter.
x + y = y + x
Representation
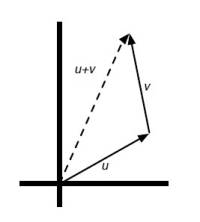
Addition of vectors over <math>\mathbb{R}</math> can be visualized using arrows.
Computation
In python:
- For two n-vectors
def addn(v, w): return [v[i]+w[i] for i in range(len(v))]
- For n n-vectors:
>>> vectorList = [[1,2,3],[1,2,3], [1,2,3]]
# How to group the number by position in the vector
>>> [[i[j] for i in vectorList] for j in range(len(vectorList[0])) ]
[[1, 1, 1], [2, 2, 2], [3, 3, 3]]
# Then add a sum to the above statement
>>> [sum([i[j] for i in vectorList]) for j in range(len(vectorList[0])) ]
[3, 6, 9]
Scalar Multiplication
Dot product
Element-wise multiplication
Element-wise multiplication is the default method when two NumPy arrays are multiplied together.
The element-wise calculation is as follows: <MATH> \mathbf{x} \odot \mathbf{y} = \begin{bmatrix} x_1 . y_1 \\\ x_2 . y_2 \\\ \vdots \\\ x_n . y_n \end{bmatrix} </MATH>
Example: <MATH> \begin{bmatrix} 1 \\\ 2 \\\ 3 \end{bmatrix} \odot \begin{bmatrix} 4 \\\ 5 \\\ 6 \end{bmatrix} = \begin{bmatrix} 4 \\\ 10 \\\ 18 \end{bmatrix} </MATH>
Others
Inner product
Cross Property
Distributivity
Scalar-vector multiplication distributes over vector addition (translation):
<MATH>\alpha(u+v)=\alpha.u+\alpha.v</MATH>
2([1, 2, 3] + [3, 4, 4]) = 2 [1, 2, 3] + 2 [3, 4, 4] = [2, 4, 6] + [6, 8, 8] = [8, 12, 14]
Addition and scalar multiplication are used to defined a a line that not necessarily go through the origin.