About
Orthogonal is linear-algebra-ese for perpendicular.
Articles Related
Definition
The squared length of the “hypotenuse” (the vector u + v) is
<math> \begin{array}{rcll} {\left \| u + v \right \|}^2 & = & \left \langle u+v,u+v \right \rangle & \\ & = & \left \langle u,u+v \right \rangle + \left \langle v,u+v \right \rangle & \text{by linearity of inner product} \\ & = & \left \langle u,u \right \rangle + \left \langle u,v \right \rangle + \left \langle v,u \right \rangle + \left \langle v,v \right \rangle & \text{by symmetry and linearity of inner product} \\ & = & {\left \| u \right \|}^2 + 2 \left \langle u,v \right \rangle + {\left \| v \right \|}^2 & \text{by symmetry of inner product} \\ \end{array} </math>
Thus following the Pythagorean Theorem u and v are orthogonal when <MATH>\left \langle u,v \right \rangle = 0</MATH>
then:
- the Pythagorean Theorem for vectors becomes:
<MATH>{\left \| u + v \right \|}^2 = {\left \| u \right \|}^2 + {\left \| v \right \|}^2</MATH>
- every vector v is orthogonal to u when u is the zero vector.
Property
- Property O1: If u is orthogonal to v then u is orthogonal to <math>\alpha v </math> for every scalar <math>\alpha</math> .
- Property O2: If u and v are both orthogonal to w then u + v is orthogonal to w.
Example
- [1, 2] · [2,-1] = 0 so [1, 2] · [20,-10] = 0
- Second Example:
[1, 2, 1] . [1,-1, 1] = 0
[0, 1, 1] . [1,-1, 1] = 0
----------------------------------------
([1, 2, 1] + [0, 1, 1]) . [1,-1, 1] = 0
Type
Mutual
<math>v_1, \dots, v_n</math> are mutually orthogonal if <math>v_i</math> is orthogonal to <math>v_j</math> for every pair <math>i,j</math> such that <math>i \neq j</math> .
Example: <math>[1, 2, 1], [1,−1, 1], [1, 0,−1]</math> are mutually orthogonal: <MATH> \begin{array}{rrrr} \langle & [1, 2, 1], & [1,−1, 1] & \rangle & = & 0 \\ \langle & [1, 2, 1], & [1, 0,−1] & \rangle & = & 0 \\ \langle & [1,−1, 1], & [1, 0,−1] & \rangle & = & 0 \end{array} </MATH>
Lemma: If <math>v_1, \dots, v_n</math> are mutually orthogonal then, for any scalars <math>\alpha_1, \dots, \alpha_n</math> : <MATH> {\| \alpha_1.v_1, \dots, \alpha_n.v_n \|}^2 = {\alpha_1}^2.{\| v_1 \|}^2 + \dots + {\alpha_n}^2.{\| v_n \|}^2 </MATH>
Mutually orthogonal nonzero are independent
Mutually orthogonal nonzero vectors are linearly independent
Proof: Let <math>v_1^* , \dots , v_n^*</math> be mutually orthogonal nonzero vectors, then they are linearly independent if the coefficient <math>\alpha_0, \alpha_1 , \dots , \alpha_n</math> are null in the following statement: <MATH>0 = \alpha_0 v_0^* + \alpha_1 v_1^* + \dots + \alpha_n v_n^* </MATH>
To show that <math>\alpha_0</math> is zero, take inner product with <math>v_0^*</math> on both sides:
<MATH> \begin{array}{rrl} \langle v_0^*, 0 \rangle & = & \langle v_0^*, \alpha_0 v_0^* + \alpha_1 v_1^* + \dots + \alpha_n v_n^* \rangle \rangle \\ 0 & = & \alpha_0 \langle v_0^*, v_0^* \rangle + \alpha_1 \langle v_0^*, v_1^* \rangle + \dots + \alpha_n \langle v_0^*, v_n^* \rangle \\ 0 & = & \alpha_0 {\| v_0^* \|}^2 + \alpha_1 0 + \dots + \alpha_n 0 \\ 0 & = & \alpha_0 {\| v_0^* \|}^2 \\ 0 & = & \alpha_0 {\| v_0^* \|}^2 \\ \end{array} </MATH> Since <math>v_0^*</math> is nonzero, the only solution is <math>\alpha_0 = 0</math>
Operations
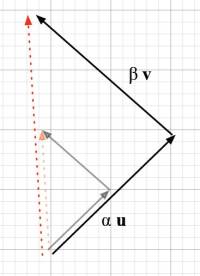
Scaling
Scaling orthogonal vectors gives orthogonal vectors. If u is orthogonal to v then, for any scalars <math>\alpha, \beta</math> : <MATH> {\left \|\alpha u + \beta v \right \|}^2 = \alpha^2 {\left \|\alpha u \right \| }^2 + \beta^2 {\left \|\alpha v \right \| }^2 </MATH>