About
How to find the closest point on a line from a point ?
How to find the vector on the line that best approximates the given vector b (the closest point on the line)
Articles Related
Lemma
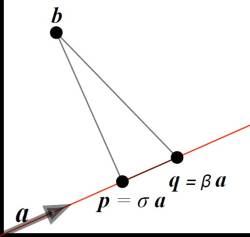
- Let b be a vector
- Let a be a non-zero vector. The set <math>\{ \alpha.a : \alpha \in \mathbb{R}\}</math> is a line L
- Let p be the point on L such that b-p is orthogonal to a
then p is the point on the line that is closest to b.
Among all the points on the line <math>\{ \alpha.a : \alpha \in \mathbb{R}\}</math> , the closest to b is the point p on such that b − p is orthogonal to a
Proof
x-axis
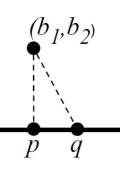 Line is the x-axis, i.e. the set <math>\{(x, y) : y = 0\}</math>
, and point is (b1, b2).
Line is the x-axis, i.e. the set <math>\{(x, y) : y = 0\}</math>
, and point is (b1, b2).
Lemma states: closest point on the line is p = (b1, 0).
- For any other point q, the points (b1, b2), p, and q form a right triangle.
- Since q is different from p, the base is nonzero.
- By the Pythagorean Theorem, the hypotenuse’s length is greater than the height.
- This shows that q is farther from (b1, b2) than p is.
Other Line
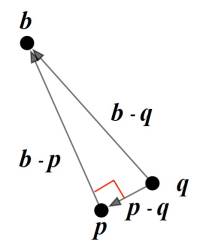 Let q be any point on L. The three points q, p, and b
form a triangle.
Let q be any point on L. The three points q, p, and b
form a triangle.
- Since p and q are both on L, they are both multiples of a, so their difference p − q is also a multiple of a.
- Since b − p is orthogonal to a, therefore, it is also orthogonal to p − q
- Hence by the Pythagorean Theorem <math> {\| b-q \|}^2 = {\| p-q \|}^2 + {\| b-p \|}^2</math>
- if <math>q \neq p</math> , then <math> {\| p-q \|}^2 > 0</math> so <math>\| b-q \| < \| b-q \|</math>
Definition
For any vector b and any vector a, define vectors <math>b^{||a}</math> and <math>b^{\perp a}</math> to be the projection of b onto Span {a} and the projection of b orthogonal to a if: <MATH> b = b^{||a} + b^{\perp a} </MATH> where:
- the point <math>b^{||a}</math> is the projection of b along a and then there is a scalar <math>\sigma \in \mathbb{R}</math> such that <math>b^{||a} = \sigma a</math>
- the point <math>b^{\perp a}</math> is a vector orthogonal to the line a. It's a projection orthogonal to a.
Then the following formulas are equivalent: <MATH> \begin{array}{lrlll} b & = & b^{||a} & + & b^{\perp a} \\ b & = & \sigma a & + & b^{\perp a} \\ b^{\perp a} & = & b & - & \sigma a \\ \end{array} </MATH>
Lemma
One-dimensional Lemma: The point in Span {a} closest to b is <math>b^{||a}</math> and the distance is the norm <math>\|b^{\perp a}\|</math> .
Corollary
For any vector b and vector a over the reals,
Computation
- To get <math>\sigma</math>
<math> \begin{array}{llll} \langle b^{\perp a}, a \rangle & = & 0 & \text{as } b^{\perp a} \text{ is orthogonal to a} \\ \langle b - b^{|| a}, a \rangle & = & 0 & \text{Substituion of b} \\ \langle b, a \rangle - sigma \langle a, a \rangle & = & 0 & \text{Using linearity and homogeneity of inner product} \\ \sigma & = & \frac{\displaystyle \langle b, a \rangle}{\displaystyle \langle a, a \rangle} & \text{Solving for } \sigma \end{array} </math>
- Function to get <math>b^{||a}</math> :
# �Find the vector (point) in Span a (line) that is closest to vector b (point):
# Projection along (or onto) a
# b || a
def project_along(b, a):
# because of floating-point roundoff error a*a > 1e-20 in place of a*a = 0
sigma = (b*a)/(a*a) if a*a > 1e-20 else 0
return sigma * a
- Function to get <math>b^{\perp a}</math> :
# Projection to a
# b perp a
def project_orthogonal(b, a):
return b - project_along(b, a)
Example
a = [6, 2] and b = [2, 4].
The closest point on the line <math>\{ \alpha a : \alpha \in \mathbb{R}\}</math> is the point <math>b^{||a} = \sigma a</math> where:
<MATH> \begin{array}{rrr} \sigma & = & \frac{a.b}{a.a} & = & \frac{6.2 + 2.4}{6.6 + 2.2} & = & \frac{20}{40} & = & \frac{1}{2} \end{array} </MATH>
thus:
- the closest point is <math>\frac{1}{2} [6,2]</math>
- the distance to b is: <math>\| b^{\perp a} \| = \| [2,4]-[3,1] \| = \|[-1,3]\| = \sqrt{(-1.-1+3.3)} = \sqrt{10} = 3,5</math>