About
complex numbers in Python
Python uses 'j' for the imaginary unit, not 'i'.
Articles Related
Snippet
- Type Complex
>>> 1j
1j
>>> type(1j)
<class 'complex'>
- Addition
>>> (3 + 1j) + (2 + 2j)
(5+3j)
>>> x = 1+3j
>>> x + 1
(2+3j)
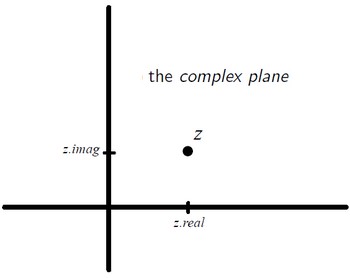
Complex Plane
The real and imaginary parts of a complex number can be interpreted as x and y coordinates in the complex plane forming a point.
- Coordinates
>>> x = 1+3j
>>> x.real # real number coordinates
1.0
>>> x.imag # imaginary number coordinates
3.0
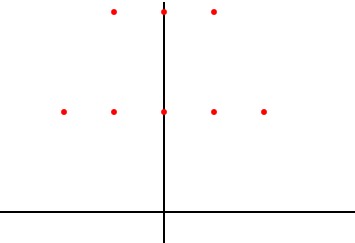
- Plot
import matplotlib.pyplot as plt
L=[-2+2j,-1+2j,0+2j,1+2j,2+2j,-1+4j,0+4j,1+4j]
X = [x.real for x in L]
Y = [x.imag for x in L]
plt.scatter(X,Y, color='red')
plt.show()
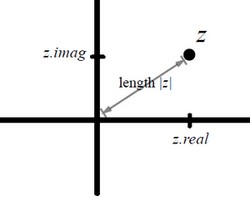
- Absolute value of z = distance from the origin to the point z in the complex plane. (In Mathematics - Mathese, |z|)
>>> abs(1+2j)
2.23606797749979
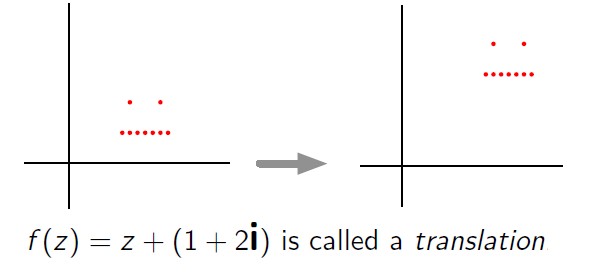
Translation
- Geometric interpretation of f (z) = z + (1+2i)?
- Increase each real coordinate by 1 and increases each imaginary coordinate by 2.
- A translation can “move” the picture anywhere in the complex plane
Translation in general:
f (z) = z + z0
where:
- z0 is a complex number.
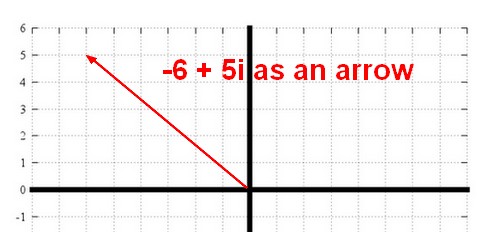
Arrow
- Complex Number as an arrow
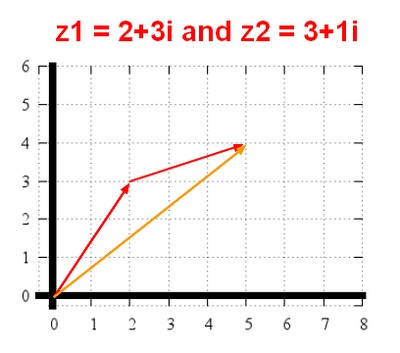
Composition (Addition)
They correspond to translations f1(z) = z + z1 and f2(z) = z + z2. Functional composition:
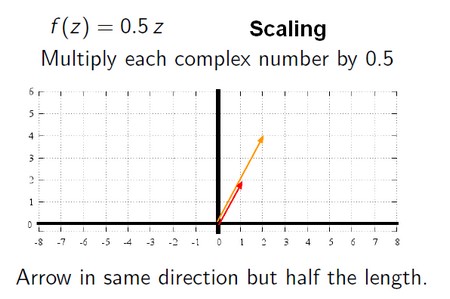
Multiplication
Scaling
Multiplying complex numbers by a positive real number
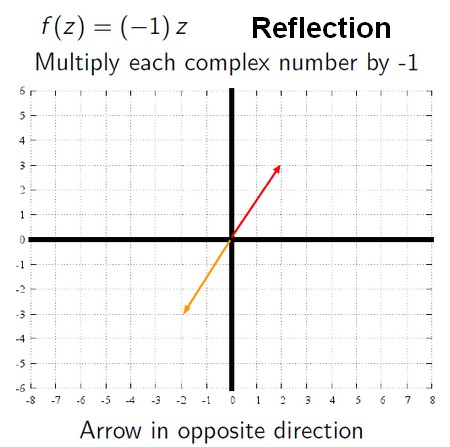
Reflection
plot({-1*z for z in L})
By i: rotation by 90 degrees
plot({1j*z for z in L})
Rotation
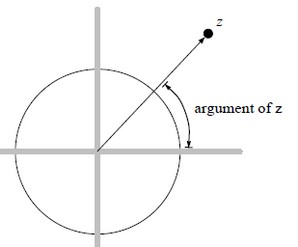
Rotating a complex number z means increasing its argument.
Argument of z is the angle in radians between z arrow and the x axis (1 + 0i arrow).
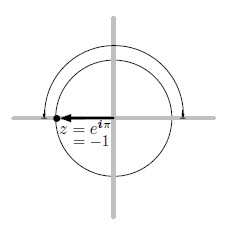
Euler’s formula: For any real number ,
is the point z on the unit circle with argument
.
e = 2.718281828…
When , z = -1
Every complex number can be written in the form
where:
- r is the absolute value of z
is the argument of z
To augment the argument of z, we use exponentiation law <math>e^a * e^b = e^{a+b}</math>
does a rotation by angle
- Rotation of 45 degrees
from math import e, pi
plot({e**(45j)*z for z in L})
- Circle with a rayon of 2
r = 2
circle = 2*pi
plot([r*e**(t*circle/20*1j) for t in range(20)])