About
A learning algorithm is said to overfit if it is:
- more accurate in fitting known data (ie training data) (hindsight) but
- less accurate in predicting new data (ie test data) (foresight)
Ie the model do really wel on the training data but really bad on real data. If this case, we say that the model can't be generalized.
In statistics and machine learning, overfitting occurs when a statistical model describes random error or noise instead of the underlying relationship.
- “Overfitting” is when a classifier fits the training data too tightly.
- Such a classifier works well on the training data but not on independent test data.
- Overfitting is a general problem that plagues all machine learning methods.
Low error on training data and high error on test data
Overfitting occurs when a model begins to memorize training data rather than learning to generalize from trend.
The more difficult a criterion is to predict (i.e., the higher its uncertainty), the more noise exists in past information that need to be ignored. The problem is determining which part to ignore.
Overfitting generally occurs when a model is excessively complex, such as having too many parameters relative to the number of observations.
When your learner outputs a classifier that is 100% accurate on the training data but only 50% accurate on test data, when in fact it could have output one that is 75% accurate on both, it has overfit.
Overfitting is when you create a model which is predicting the noise in the data rather than the real signal.
Articles Related
Graphic Representation
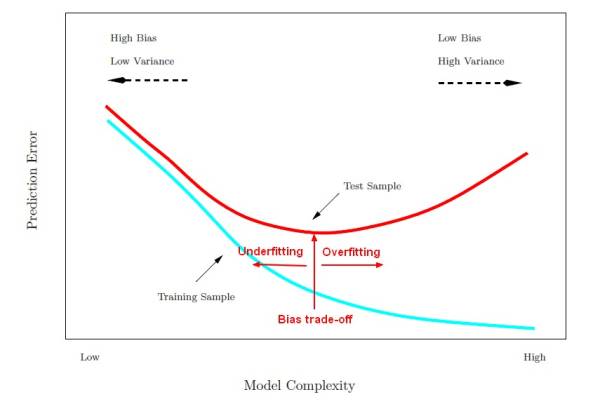
The ingredients of prediction error are actually:
- bias: the bias is how far off on the average the model is from the truth.
- and variance. The variance is how much that the estimate varies around its average.
Bias and variance together gives us prediction error.
Model Complexity vs Prediction Error
where:
- Model complexity are important techniques to fit better a data set (ie to reduce the prediction error).
Model complexity decreases prediction error until a point (the bias trade-off) where we are adding just noise. The trainer error goes down as it has to, but the test error is starting to go up. That's over fitting.
We want to find the model complexity that gives the smallest test error.
Bias Variance Matrix
See:
Example
If the number of parameters is the same as or greater than the number of observations, a simple model or learning process can perfectly predict the training data simply by memorizing the training data in its entirety, but such a model will typically fail drastically when making predictions about new or unseen data, since the simple model has not learned to generalize at all.
It' easy to demonstrate “overfitting” with a numeric attribute. Example with the weather data set and the temperature numeric attribute
if temperature in (83, 64, 72, 81, 70, 68, 75, 69, 75) then 'Play'
else if temperature in (65, 71, 85, 80, 72) then 'Don''t Play'
There is one condition by observation and therefore the rules fit to much the (training) data.
How to
Measure
How badly algorithms overfit can be judged in terms of the apparent performance improvement between training set(s) and test set(s) with the help of the following measures:
- standard errors of estimators where standard error is the standard deviation of the new estimates under resampling. (ie by getting new samples over and over again and by recomputing our estimate).
Ideally, in order to calculate them, we get a new test sample from the population and see how well our predictions do.
But it's very often not possible to have a new one then if:
- we have a large test set, we can resample
- or we don't have a large test set, we can adjust the training error to get the test error with the help of mathematical methods that are going to increase it by a factor that involves the amount of fitting that we've done to the data and the variance. These methods could be:
- the Cp statistic,
- the AIC
- and the BIC.
Difference between the fit on training data and test data measures the model’s ability to generalize.
A algorithm that get 100% accurate on the training set overfits dramatically.
Avoid
An algorithm is less likely to overfit:
- with simple decision boundaries (ie simple model)
- when it relies on a small number of data point. See support vectors
By using several algorithm in order to make the good decision is also a good solution to avoid over-fitting.
In order to avoid overfitting in a algorithm, it is necessary to use additional techniques
- on parameters:
Model and Overfitting
boosting seems to not overfit (Why boosting does'nt overfit)
Glossary
Robust
A learning algorithm that can reduce the chance of fitting noise is called robust.
Generalize
Is the model able to generalize ? Can the model deal with unseen data, or does it overfit the data?
Generalizing is finding pattern in order to not overfit.
See Evaluation
A good generalization helps us to see the meaning of each feature, and puts the whole into a broader perspective.