About
A real number plus an imaginary number is a complex number.
Complex numbers are a number system.
A complex number has a real part and an imaginary part. <MATH>\text{complex number} = \text{(real part)} + \text{(imaginary part)} i</MATH>
where:
- i is an imaginary number
Complex Numbers are the intellectual ancestors of vectors.
Complex numbers are convenient to apply geometric transformation (such as rotation, scaling and translation) in two dimensions.
Articles Related
Visualization
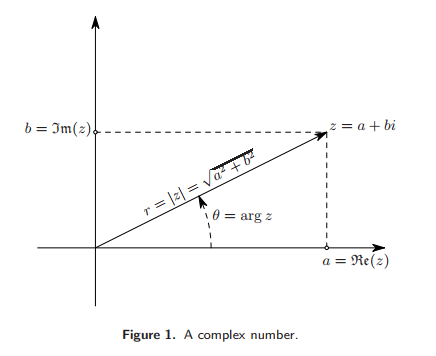
Since any complex number is specified by two real numbers one can visualize them by plotting a point with coordinates (a,b) in the plane for a complex number a + bi. The plane in which one plot these complex numbers is called the Complex plane, or Argand plane.
- Real numbers lie on the horizontal axis
- Imaginary numbers lie on the vertical axis
Properties
- Length: |z| is the distance from the origin to the point z in the complex plane.
<MATH> |z| = \sqrt {a^2 + b^2} </MATH>
- Angle: The angle θ is called the argument of the complex number z. Notation:
<MATH> arg z = θ </MATH>
Law
when you multiply complex numbers:
- their lengths get multiplied
- and their arguments get added.
Example
- Problem: <math>(x -1)^2 = -9</math>
- Solution: <math>x = 1 + 3 i</math>
Documentation / Reference
* https://www.math.wisc.edu/~angenent/Free-Lecture-Notes/freecomplexnumbers.pdf