About
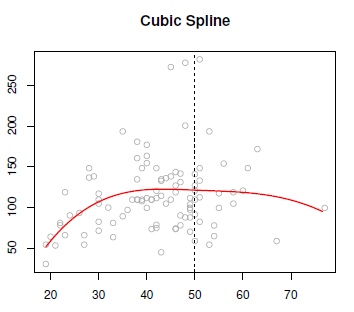
Cubic splines is a step cubic piecewise polynomial in the left and the right and continuous at the knot.
There's the following constraints:
- The first derivatives continues at the knot,
- and the second derivatives continues at the knot.
We couldn't make the third derivative continuous, because then it would just be a global cubic polynomial. It's believed that a cubic spline, the discontinuity which exists in the third derivative is not detectable by the human eye.
The degree of Statistics - Piecewise polynomials is 2 because it's a third degree polynomial.
Articles Related
Definition / Representation
A cubic spline with knots at <math>\xi_k</math> with <math>k = 1, \dots, K</math> is a piecewise cubic polynomial with continuous derivatives up to order 2 at each knot.
As a linear spline, this model can be represented with truncated power basis (functions|expansion|transformation) in the original variables
<MATH> y_i = \beta_0 + \beta_1.b_1(x_i) + \beta_2.b_2(x_i) + \dots + \beta_{K+3}b_{K+3}(x_i) + \epsilon_i </MATH>
where the <math>b_k</math> are basis functions and are:
- the variable itself. The first basis functions is just the variable itself
<MATH> \begin{array}{rll} b_1(x_i) & = & x_i \\ \end{array} </MATH>
- the variable squared
<MATH> \begin{array}{rll} b_2(x_i) & = & x_i^2 \\ \end{array} </MATH>
- the variable cubed
<MATH> \begin{array}{rll} b_3(x_i) & = & x_i^3 \\ \end{array} </MATH>
- and additional variables that are a collection of truncated basis transformation functions at each of the knots. They are called truncated power functions and this one is to power 3 (cubic).
<MATH> \begin{array}{rll} b_{k+3}(xi) & = & (xi - \xi_k)_+^3 \text{ where } k = 1, \dots, K \\ \text{where the ()+ means positive part. i.e. } (xi - \xi_k)^3_+ & = & \left\{ \begin{matrix} (xi - \xi_k)^3 & \text{ if } x_i > \xi_k & \\ 0 & \text{Otherwise} & \text{It's not allowed to go negative.} \end{matrix} \right. \end{array} </MATH>
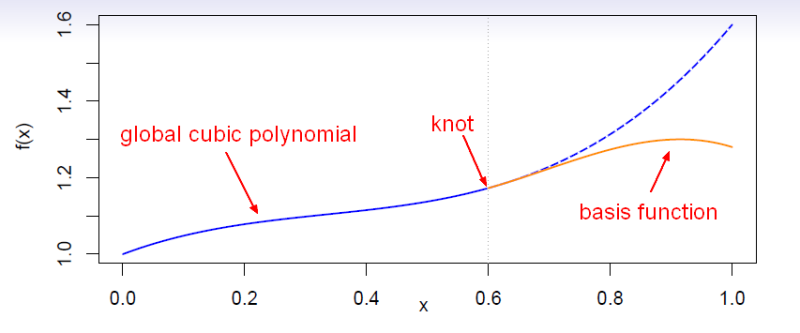
Plot
At the knot, the basis function:
- is 0
- got 0 first derivative and 0 second derivative.
Therefore, when we add it, we don't change the derivatives of the function and so has the required continuity of a cubic spline.
Degree of freedom
A cubic spline with K knots has K plus 4 parameters or degrees of freedom.